Note: This example uses Protelis version 0.1.0, while current version is 13.1.0-dev0f+6aed1deb. As such, the provided code might not work with newer releases.
This example has been presented in the paper:
Peer-to-peer route planning
When two people want to meet up at a large event, they may be hampered when a pre-arranged rendezvous point turns out to be inconvenient, while any centralized services for real-time coordination are overwhelmed by demand. Peer-to-peer calculations between participating devices could guide the two friends to meet at an intermediate location, regardless of the continued movement of the two friends and participating devices in the area.
Code samples and illustrations from a simulation
Using some of Protelis' special operators and syntax, a small number of functions can be defined and applied to variables. Alice and Bob can be directed toward each other (red dots) through the peer-to-peer calculations performed on participating devices (blue dots).
The function distanceTo computes the minimum distance from any device to the nearest source device (a device where source is true).
The field d is initially Infinity everywhere, but is set to 0 on sources and set to the minimum across neighbors of the sum of d and the estimated distance to the current device.
def distanceTo(source) {
rep(d <- Infinity) {
mux (source) { 0 }
else { minHood(nbr(d) + nbrRange) }
}
}
The function descend follows the gradient of a potential field down from a source.
Given an original device (self) and a potential potential field,
this function builds a path of intermediate devices connecting the original device with the source of the potential field.
The original device is marked as part of the path.
Other devices are identified as being on the path if one of their neighbors is already on the path,
and they are the closest of that neighbor’s neighbors to the destination.
def rendezvous(person1, person2) {
descend(person1 == owner, distanceTo(person2) == owner))
}
The rendezvous function uses the descend function to identify the path between two people, whose devices have been marked with the owner property.
def rendezvous(person1, person2) {
descend(person1 == owner, distanceTo(person2) == owner))
}
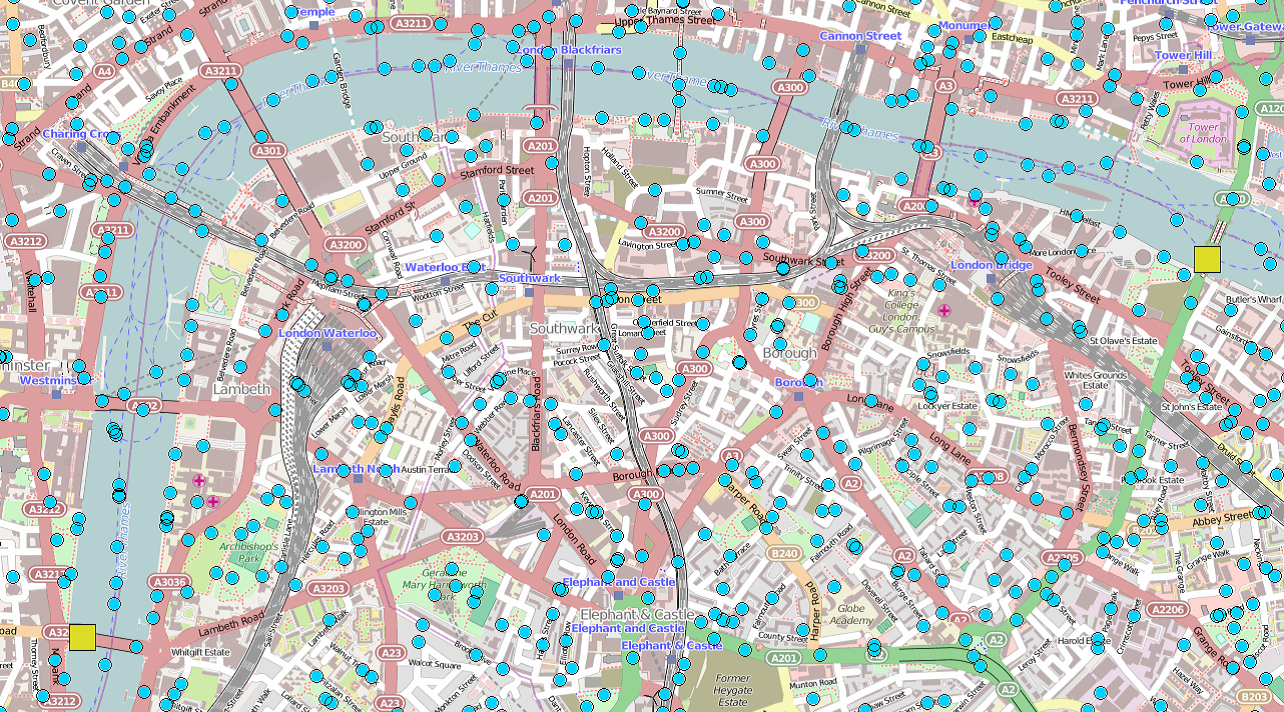
Imagine an initial configuration where a number of individuals carrying participating devices (blue dots) are attending a large event, and two of them (Alice and Bob, as two yellow squares) wish to meet up.
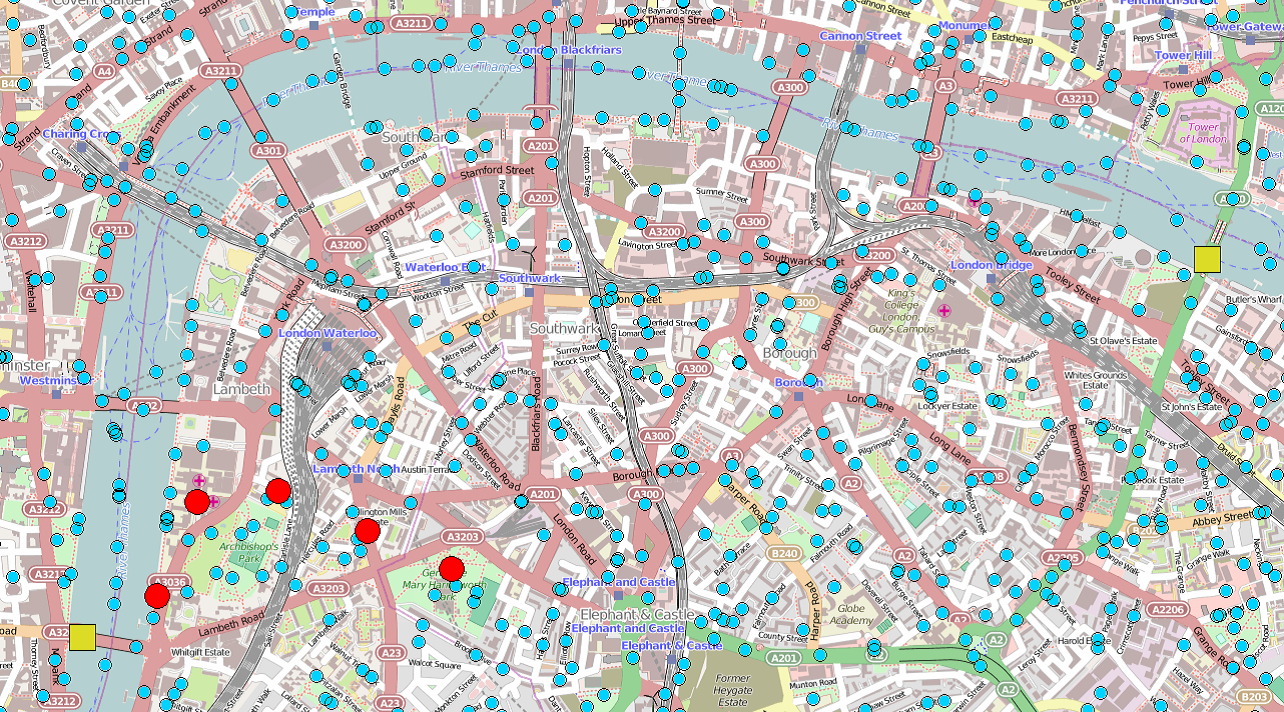
Alice and Bob activate their rendezvous application, and nearby devices that are on the shortest path between them start to be selected as part of their rendezvous path (red dots).
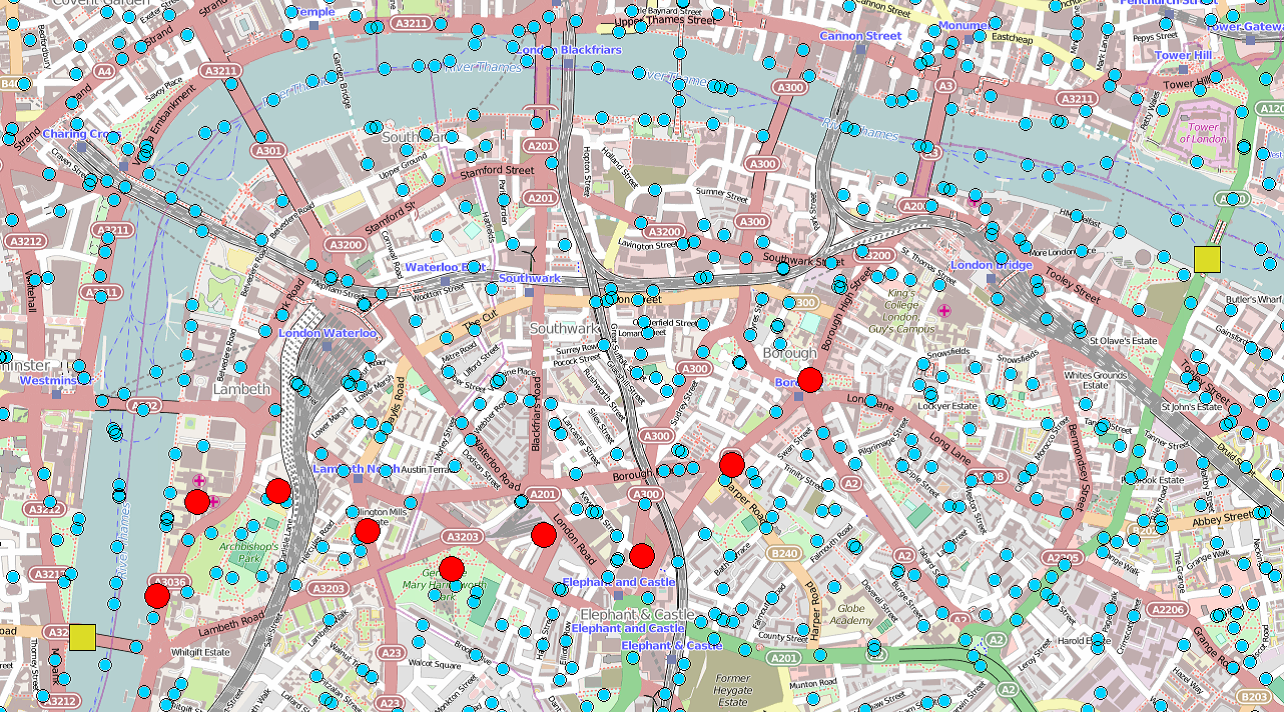
No central information service is needed for peer-to-peer calculation of the shortest path.
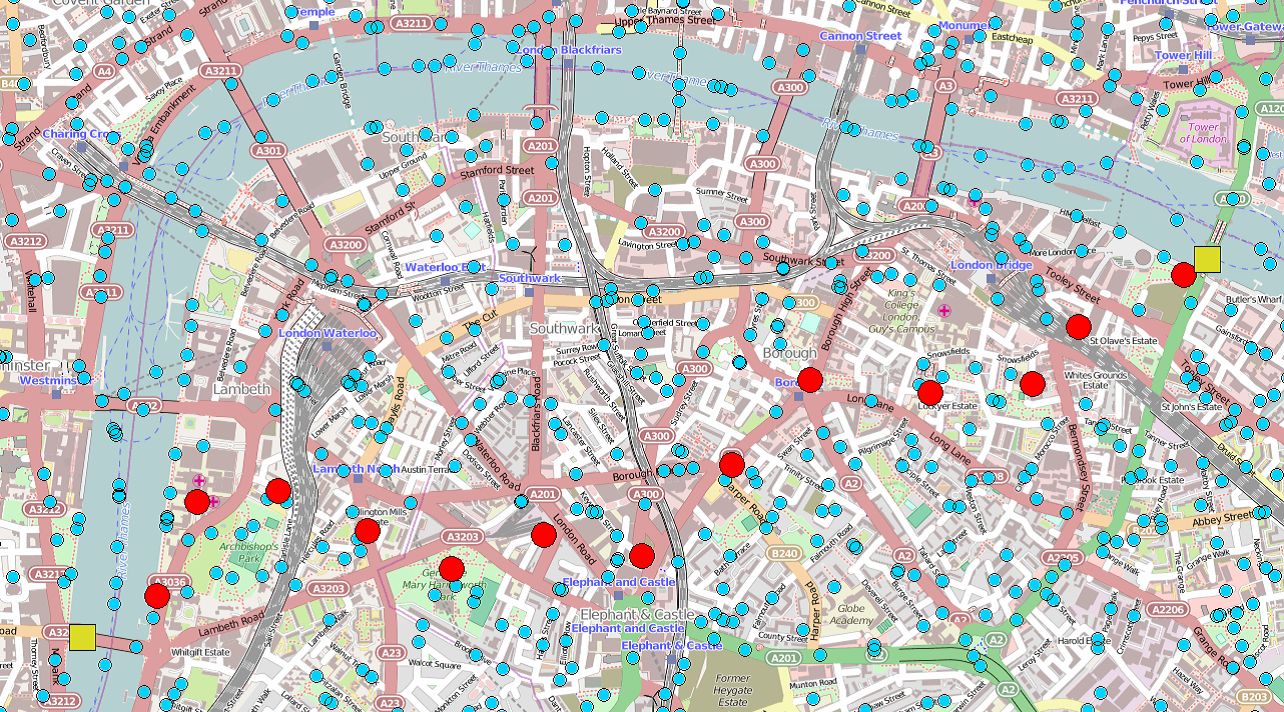
The complete path is calculated, and will update automatically as Alice and Bob walk toward each other, and as intermediate devices move around.